Задача для первоклассников, которую не могут решить взрослые

Ответ

Для решения данного математического примера необходимо следовать определенным правилам приоритета операций. Правило гласит, что сначала выполняются операции в скобках, затем умножение и деление, а затем сложение и вычитание.

В данном примере, сначала нужно выполнить операцию в скобках:

Затем нужно выполнить деление 6 на 2:

И, наконец, умножить результат на 3:

Таким образом, ответ на данный математический пример равен 9.

Правильный ответ на данный математический пример равен 9.

Важно помнить, что приоритет операций является основой для решения математических примеров. Если вы сомневаетесь в правильности решения, всегда можно воспользоваться калькулятором или обратиться к учителю или эксперту в данной области

Монти Холл и три шкатулки

Перед вами стоят три одинаковых закрытых шкатулки, в одной из них лежит много денег, а две других — пустые. Можно выбрать любую шкатулку, но сразу открывать нельзя. Затем ведущий игры берёт одну из оставшихся шкатулок, открывает и показывает, что она пустая.

Теперь у вас есть выбор: оставить себе ту шкатулку, которую вы выбрали с самого начала, или поменять её на оставшуюся неоткрытую. Как лучше поступить?

Отбросим в сторону эмоции, интуицию и прочую эзотерику и начнём решать эту задачу как программисты — дадим нашим шкатулкам имена:

Выбранная — шкатулка, которую мы выбрали с самого начала;
Пустая — ту, которую открыли после нашего выбора и показали, что она пустая;
Неизвестная — одна из двух невыбранных нами шкатулок, которая осталась закрытой, и на которую можно поменять нашу.

Изначально вероятность того, что вы выбрали сразу шкатулку с деньгами — 33%, потому что в самом начале у каждой шкатулки одинаковые шансы. Но теперь всё зависит от того, случайно ли ведущий открыл Пустую шкатулку, или знал заранее, что в ней ничего нет. Именно от этого будет зависеть, как нужно поступить.

Если пустую шкатулку открыли случайно

Допустим, ведущий игры не знал ничего о содержании шкатулки. То есть, открывая одну из невыбранных, он мог открыть и шкатулку с деньгами.

Раз этого не произошло и никто действительно заранее не знал, в какой из шкатулок деньги, то у них теперь равные шансы на победу: вместо ⅓ они стали равны ½. У обеих шкатулок теперь одинаковая вероятность оказаться с деньгами, поэтому менять шкатулки смысла нет: математически это никак не увеличит ваши шансы. Всё, что будет дальше, уже эзотерика.

Итого. Если Пустую шкатулку открыли случайно и никто не знал заранее, что она пустая, то верная стратегия будет такой: оставить себе Выбранную шкатулку.

Пустую шкатулку выбрали специально

Теперь рассмотрим ситуацию: ведущий знал, что открытая шкатулка окажется пустой. Он изначально знал, где лежат деньги, и специально выбрал пустую шкатулку, чтобы её открыть.Это совсем другая ситуация, хотя может показаться, что она такая же, как и в первом случае. На самом деле нет. Там у нас появлялась новая информация, потому что никто не знал, где лежат деньги. Новая информация заставила пересчитать шансы.

В этом случае новой информации нет, потому что шкатулка с деньгами известна заранее. А раз новой информации нет, то у Выбранной шкатулки, шансы на победу как были ⅓, так и остались. А теперь начинается магия теории вероятности: шансы на победу у Неизвестной шкатулки выросли вдвое!

Дело тут вот в чём. Раз изначально у всех шкатулок шансы были равны, то для каждой шкатулки они составляли ⅓. Когда нам умышленно открыли Пустую шкатулку, то вероятность Выбранной шкатулки не поменялась (так как новой информации нет), а вероятность Неизвестной шкатулки выросла вдвое:

⅓, которая была изначально + ⅓, которая перешла от Пустой шкатулки к Неизвестной = ⅔.

Нет новой информации — шансы не пересчитываются, а перераспределяются между теми шкатулками, содержимое которых заранее известно. Раз открывающий шкатулки знает, где деньги, значит, шансы перераспределяются между ними. А у вашей шкатулки как был шанс на победу ⅓, так и остался.

Итого. Если Пустую шкатулку открыли специально, правильная стратегия будет такой: поменять Выбранную шкатулку на Неизвестную. Это повысит ваши шансы на победу в 2 раза.

Важно понимать, что мы говорим о шансах и вероятностях, а не о конкретном единичном случае. Иначе говоря, эта стратегия будет иметь смысл, если сыграть много игр с одинаковыми условиями: сто, триста, тысячу

На одной конкретной игре эффект вероятностей не будет заметен. Поэтому вместо азартных игр мы рекомендуем коммерческое программирование.

Как решается пример

Если пример подразумевает, что нужно выполнять действия последовательно, необходимо поставить знак умножения. С ним сложность записи не увеличивается, красота и понятность примера не теряются.

Так как знак умножения в исходном примере 36:3(8-6)/6 не указан, автор вкладывал в выражение другую последовательность действий.

Если же мы захотим строго записать пример, в котором нужно делить на все выражение 3(8–6), тогда его придется записать так:

Пример теперь выглядит громоздко и неуклюже из-за двойных скобок. Поэтому для такого сценария вычислений будет корректна запись:

Знак умножения опущен для того, чтобы показать цельность двух объектов и чтобы не нагромождать выражение двойными скобками.

Следовательно, ответом будет 1.

Бабушка и помидоры

Бабушка решила заняться фермерским хозяйством — выращивать и продавать помидоры. Она насобирала 100 кг томатов, погрузила их на тележку и выставила с утра перед домом.

Помидоры, которые вырастила бабушка, на 99% состоят из воды, но на солнце часть воды испаряется сквозь кожуру. День выдался жарким, и к вечеру воды в помидорах стало уже 98%. Сколько теперь весят бабушкины помидоры?

Результат может оказаться неожиданным для вас, поэтому внимательно следите за расчётами.

Для начала рассчитаем состав помидоров с утра. В них было 99% воды. Это значит, что в них было 99 килограммов воды и 1 килограмм клетчатки. Эта клетчатка с утра занимала 1%:

100% — 99% = 1%.

По условию задачи, этот килограмм клетчатки не может испариться или исчезнуть, его вес всегда одинаковый. Испаряется только вода.

Теперь считаем состав помидоров вечером: воды было уже 98%. Это значит, что количество воды уменьшилось, но вся клетчатка осталась на месте: как был килограмм с утра, так и остался. Но изменилось процентное соотношение клетчатки к воде: сейчас тот же самый килограмм клетчатки занимает 2% общего веса. Давайте посчитаем, сколько тогда вечером весят все помидоры:

2% помидоров весит 1 килограмм, а значит 20% весят 10 килограмм.

Умножаем обе части на 5, чтобы получить полный вес. Получаем:

100% = 50 кг.

Оказывается, к вечеру вес снизился вдвое! Это неинтуитивно, но так работает математика. ¯\_(ツ)_¯

Мы не человек разупный, а девятикантропы: 1. Мальчик с пальчик и десятичное недоразумение
Жил-был скромный мальчик,
он, всё время, прятал пальчик,
2000 лет не могли его найти,
и безымянным называли
и нулем его крестили,
но проблему не решили,
только ошибками «крошили».
Место нулей его поставьте.
Ведь нули – обозначение пустоты,
а цифры около нуля обозначают степеня.
АНГЕЛ звать его, его пишите
в виде зеркальной цифры шесть,
вы не поверите – он есть!
Десятичная система должна иметь вид: 123456789 «6»=10 для сохранения разрядности, поскольку последняя цифра в каждом десятке вносится по умолчанию и приравнивается к нулю. А цифра «0» должна писаться, начиная со 101, особенную ценность, данная система, имеет для матричного исчисления

«МОЖЕШ» ПИШЕТСЯ С ь )))))))

Между однородными членами предложения надо ставить запятую, а в конце — точку.

«Можешь найти» это один член предложения (сказуемое)

это не логика а ваша фантазия про (ь) это просто глупа и бессмысленно! но по логически вы пропустили 0 (числу 0)

Саме речення і є помилкою,тому що в цифрах помилки немає)

мягкий знак в слове «можеш»ь»

Чтобы вы провалились со своими задачами=_=

ошибка и есть слово ошибка

«Даны ЧИСЛА»
Так как 1 2 3 4 5 6 7 8 9 являются ЦИФРАМИ, то следовательно ошибка заключается в присутствии здесь значений от 1-ого до 9-ти.

Слово можеш пишется так: МОЖЕШЬ

Даааа, я смотрю гений математики, ухахха
Из ряда: «я сидел на задней парте, слушал музыку в наушниках и случайно услышал что 1-9 это цифры, а не числа»

Так-то цифры и есть числа. Ты ведь наверняка слышал(а): натуральное число — число от 1 и до бесконечности. Исходя из этого, уже можно доказать выше сказанное мною.

Числа от 9 со ссылками. С каких пор цифры бывают со ссылками не в Википедии

«Можешь» пишется с мягким знаком

Да это легкотня тот кто это не знает позор слово можешь пишется с ь знаком

втор математически, не грамотный человек. 1-9 это цифры, а все остальное это числа.

Аха, неожиданно как, после кучи грамматических ошибок в задачах автор признал одну ошибку!

12345678910 11 12 13 14 15 .Ниже написано
«Найдите тут ошибку»
В чём здесь подвох!?

слово «ошибку» написано неверно

В слове ошибка все правильно потому что ж ш пиши с буквой и. Поняла?

Ошибка в слове можеш, надо писать можешь

Нужно найти ошибку,это и есть то слово на картинке (ошибку) загадка с подвохом )

слово ‘ошибка’ и есть ошибка

Слово «можешь» надо писать с мягким знаком!

Числа даются через запятую иначе — воспринимаются все как одно число.

Странный разговор двух программистов

Встречаются два программиста, которые давно друг друга не видели. У них происходит такой диалог:

— Я слышал, у тебя дети появились.

— Да, три сына.

— И сколько им лет?

— Ну… В сумме — тринадцать!

— Хм… Ты снова загадками говоришь? Ну ладно. Что ещё можешь сказать?

— Если возрасты перемножить, получится столько же, сколько окон вон у того дома.

Программист считает окна и прикидывает варианты.

— Но этого до сих пор недостаточно для ответа!

— Могу добавить, что мой старший сын — рыжий.

— Ну теперь совсем другое дело. Им … (далее следует ответ).

— Правильно!

Сколько же лет им было? И как первый смог вычислить возраст?

Если вам до сих пор кажется, что эта задача — полная дичь, мы вас понимаем. И всё-таки у неё есть чёткое, логичное и точное решение.

Суть его в том, что каждый ответ второго — уточнение или подсказка для решения. И первый задавал вопросы до тех пор, пока все подсказки не привели его к правильному ответу. Давайте проследим за ходом его мыслей.

Первый ответ говорит нам о том, что всего детей — трое. Хорошо, но явно недостаточно для того, чтобы вычислить возраст.

Второй ответ говорит о том, что в сумме детям 13 лет. Давайте запишем все возможные комбинации возрастов, которые подходят под это условие:

1 + 1 + 11 = 13

1 + 2 + 10 = 13

1 + 3 + 9 = 13

1 + 4 + 8 = 13

1 + 5 + 7 = 13

1 + 6 + 6 = 13

2 + 2 + 9 = 13

2 + 3 + 8 = 13

2 + 4 + 7 = 13

2 + 5 + 6 = 13

3 + 3 + 7 = 13

3 + 4 + 6 = 13

3 + 5 + 5 = 13

4 + 4 + 5 = 13

Остальные комбинации получаются из этих простой перестановкой возрастов.

Третий ответ — произведение возрастов равно числу окон. Кажется, что это вообще никак нам не помогает, потому что мы не знаем количества окон в доме, — но это не так. Если бы этого ответа было достаточно, то первый бы сразу назвал возраст, но раз он этого не сделал, значит, информации было недостаточно.

Давайте посмотрим на произведения всех комбинаций возрастов и попробуем понять, что же с ними не так:

1 × 1 × 11 = 11

1 × 2 × 10 = 20

1 × 3 × 9 = 27

1 × 4 × 8 = 32

1 × 5 × 7 = 35

1 × 6 × 6 = 36

2 × 2 × 9 = 36

2 × 3 × 8 = 48

2 × 4 × 7 = 56

2 × 5 × 6 = 60

3 × 3 × 7 = 63

3 × 4 × 6 = 72

3 × 5 × 5 = 75

4 × 4 × 5 = 80

Раз этого ответа про количество окон оказалось недостаточно, значит в доме было столько окон, что под это число попадали сразу несколько результатов произведений. Мы выделили их в таблице. Все остальные числа давали бы однозначный ответ про возраст, а для числа 36 есть несколько вариантов, поэтому первый сказал, что этого ему недостаточно.

Четвёртый ответ — старший сын рыжий. Цвет волос нам не так важен, как количество старших сыновей. Так как «старший сын» означает, что он такой старший один, значит, вариант 1 — 6 — 6 нам не подходит, потому что в нём старших сыновей двое. Остаётся только один вариант: 2 — 2 — 9.

Ответ: старшему сыну 9 лет, двум другим — по 2 года.

Задача №5

Мудрецы и колпаки.

Царь решил проверить своих троих мудрецов на мудрость, пригласил их и сказал: «Мудрецы, у меня есть 5 колпаков – 3 из них черные, а 2 белые. Сейчас вы закроете глаза, и я надену на ваши головы эти колпаки, при этом вы не будете знать, колпак какого цвета у вас на голове, но будете видеть колпаки других мудрецов». После осуществленных действий мудрецы открыли глаза и долго-долго молчали. Затем один из мудрецов произнес: «На моей голове черный колпак!» И он был прав.

Вопрос: как мудрец догадался?

Ответ

После того, как мудрецы открыли глаза, они долго-долго молчали, что является ключевой фразой, потому что если бы один из мудрецов увидел на двух других белые колпаки, то он бы сразу понял, что на нем черный колпак. Поэтому первый важный вывод: на головах мудрецов нет двух белых колпаков. Соответственно, есть либо один белый, либо вообще нет.

Далее. Наши мудрецы: А, Б и В. Догадался о том, что на нем черный колпак мудрец А. Проследим ход его мыслей:

«Предположим на мне белый колпак, тогда мудрец Б, глядя на меня рассуждал бы так: «Возможно, на мне белый колпак, получается на мудреце А тоже белый колпак, тогда мудрец В сразу же сказал бы, что на нем черный колпак, но этого не происходит, значит на мне черный колпак», но ведь он не говорит, что на нем черный колпак! Значит, мое предположение неверно, и он не видит на мне белого колпака. Значит мой колпак черный!»

Да, такая вот интересная задача.

Помимо задач хотелось бы предложить загадки с подвохом. По возможности уделите время их решению, это будет увлекательно.

Какие есть варианты решения

У примера есть два ответа. Или нет — ответ в конце статьи!

Для математиков начальных классов ответ — 4	Для учеников средней школы ответ — 1
Если в примере указать знак умножения, тогда все становится однозначно: действия выполняются по порядку, результат равен 4.	В примере, который мы разбираем, знак умножения опущен. Из-за этого читать пример можно по-разному: либо нужно делить только на 3, либо нужно делить на произведение 3 и (8 – 6).

Образовательная платформа компании Skyeng помогает учителям преподавать в свое удовольствие: готовые интерактивные упражнения и карточки с теорией, возможность использовать свои наработки, автоматическая проверка домашних заданий.Больше подробностей о преподавании математики у нас в статьях:

Мотивируйте школьников на пути к ЕГЭ
и получайте от 48 000 ₽ и больше

Заполнить анкету

Почему знак умножения опускается

Первая причина — упростить запись. Это легко заметить в выражениях 2x, xy, abc, которые выглядят приятнее, чем 2 * х, x * y, a * b * c.

Вторая причина — показать, что перед нами один объект. Это хорошо иллюстрирует тема одночленов в математике 7-го класса. Например, 2abc — это одночлен в стандартном виде, а 2a * bc — это уже произведение двух одночленов, результатом которого станет выражение 2abc.

Вторая причина станет ключом к разгадке примера, который мы разбираем.

Рассмотрим выражение: 2х : 2х.

Здесь знаки умножения опущены не только для краткости. Благодаря этому мы видим частное одночленов, результатом которого становится 1.

Если бы перед нами было выражение 2 * х : 2 * х, то результат был бы х^2. Здесь сработали правила последовательного выполнения действий.

Третья причина — математики опускают знаки действий для краткости и красоты.

Рассмотрим пример, когда красота важнее правильной записи

В 8 классе школьники изучают основное тригонометрическое тождество sin2x + cos2x = 1. Эта запись полностью противоречит смыслу, который она несет. Такое использование квадрата подразумевает sin(sin(x)) — применение функции к самой себе.

Корректная запись была бы такой: (sin(x))2 + (cos(x))2 = 1.

Для простоты и красоты математики пошли на такой шаг с позицией, что их правильно поймут. И благодаря этому мы знаем основное тригонометрическое тождество в том виде, в котором его дают в школьных учебниках.

У нас есть и другие материалы по математике:

Как решается пример

Следовательно, ответом будет 1.

Почему пример 36:3(8-6)/6 некорректен

При создании учебников и литературы для знаков умножения действует правило: знак умножения опускается, если ошибка невозможна.

Речь идет о единственной интерпретации выражения. В примерах, которые мы приводили выше, ошибки не случаются — их понимают одинаково.

В примере 36:3(8-6)/6, который стал поводом для этого материала, случились разногласия.

Следовательно, знак умножения в данном случае опущен некорректно.

Решение примера

В данном примере у нас есть скобки, поэтому сначала нужно выполнить операцию внутри них:

Теперь у нас есть упрощенное выражение:

Следуя правилу приоритета операций, сначала нужно выполнить деление:

Теперь у нас осталось умножение:

Итак, ответ на данный математический пример равен 9.

Правильный ответ на данный математический пример равен 9.

Программисты и странное знакомство

Два джуна, Аркадий и Борис, только что познакомились с Катей и спрашивают, когда у неё день рождения. Катя — технический директор и не любит отвечать прямо, поэтому предложила им десять возможных дат:

15 мая,

16 мая,

19 мая,

17 июня,

18 июня,

14 июля,

16 июля,

14 августа,

15 августа,

17 августа.

Затем она сказала Аркадию месяц своего рождения, а Борису — день. После этого состоялся диалог:

Аркадий: Я не знаю, когда у Кати день рождения, но я знаю, что Борис тоже не знает.

Борис: Хе-хе, сначала я тоже не знал, когда у неё день рождения, но теперь знаю.

Аркадий: А, ну теперь и я знаю.

Борис: Само собой.

Как они снова это сделали?

Оставим за скобками, что они могли просто сообщить друг другу день и месяц.

Здесь нет никакой магии — чистая логика. Разберём диалог по репликам.

Аркадий: я не знаю, когда у Кати день рождения, но я знаю, что Борис тоже не знает

Аркадий знал только месяц, но был уверен, что Борис про месяц не догадается — рассмотрим это подробнее.

Если бы Катя назвала Борису 18-е или 19-е число, Борис бы сразу понял, что это 19 мая или 18 июня, потому что эти числа встречаются только один раз. Но Аркадий мог гарантировать, что Борис не знает точной даты, только в одном случае — если бы день рождения был в июле или в августе. Иначе есть риск, что Борису назвали 19-е число из мая или 18-е из июня.

Получается, что это не может быть май или июнь, иначе нет стопроцентной гарантии, что Борису не назовут 18-е или 19-е число. Остаются июль и август.

Борис: хе-хе, сначала я тоже не знал, когда у неё день рождения, но теперь знаю

На этом моменте у нас остались такие даты: 14 июля, 14 августа, 16 июля, 15 августа, 17 августа. Борис понял, что Аркадий исключил май и июнь, и это дало ему нужную подсказку по месяцу. Получается, что это было точно не 14 число, потому что оно встречается по одному разу в каждом оставшемся месяце, и ответ Аркадия ничего бы Борису не дал.

Остаются 16 июля, 15 августа и 17 августа. Именно среди них и есть день рождения Кати, месяц которого Борис однозначно определил по числу. Мы с вами пока его ещё не знаем, но Борис в этот момент его уже вычислил.

Аркадий: А, ну теперь и я знаю

После ответа Бориса Аркадий понял, что Борис оставил себе эти три даты и по числу догадался о месяце. Нам же вместе с Аркадием нужно сделать наоборот — по месяцу догадаться о числе.

16 июля, 15 августа, 17 августа.

По условию, Аркадий знает месяц, и раз он после ответа Бориса догадался о точной дате, то это был июль. Дело в том, что если бы Аркадию назвали август, то он бы не смог однозначно выбрать, 15 или 17 августа отмечается день рождения. А раз так, то остаётся июль, а единственное оставшееся число в июле — 16-е.

Получается, что день рождения Кати — 16 июля, а Борис и Аркадий снова получают приз за самые странные диалоги.

Но пошла ли она с кем-то из них на свидание?

Задача для детей 7 лет

Задача № 1:

В поезде находилось некоторое количество пассажиров.

На первой остановке вышло 19 человек.

На этой же остановке в салон поезда вошло 17 новых пассажиров.

Теперь в вагоне оказалось 63 пассажира.

Вопрос: Сколько всего пассажиров находилось в поезде в начале?

Задача № 2:

А вот еще одна задача, которую легко решают большинство первоклассников. А вот у взрослых эта задача вызывает споры.

Итак, посмотрите на эту картинку. В каком направлении движется автобус? Влево (A) или вправо(B)?

Отвечая на вопрос, помните о том, что вы должны рассуждать, как рассуждает 7-летний ребенок, когда видит этот автобус.

А теперь посмотрите на ответы к обеим задачам и сравните с их с вашими ответами. Совпали ли они?

Ответ к задаче № 1:

Изначально в салоне было 65 пассажиров!

Причем, задачу можно решить двумя способами:

Способ № 1:

Вы можете идти от обратного, и вычесть из 63 17 пассажиров, которые вошли, а затем добавить 19 пассажиров, которые вышли на первой станции.

Способ № 2:

Или вы можете найти разницу между 19 и 17 (2 человека). Затем добавить ту разницу к 63, тому количеству пассажиров, которые у нас имеются после того, как все вышли и зашли в поезд.

Какой бы метод вы ни использовали, в итоге вы должны получить один и тот же ответ: 65 пассажиров!

Задачка кажется довольно простой, не так ли?

Однако, несмотря на кажущуюся простоту, большинство взрослых людей не сразу справились с её решением. Некоторых смутила формулировка вопроса, и они стали искать подвох.

Некоторые вычитали 17 из 63, придя к ответу, что изначально в поезде было 46 человек.

Ответ к задаче № 2:

Взрослые склонны искать сложное в самой простой задаче. Это часто затрудняет решение проблемы. Иногда нужно просто взглянуть на задачку глазами ребенка, и правильное решение придёт само собой.

Итак, ответ на вопрос об автобусе — А. Как мы это узнали? В чем заключается разгадка?

Еще раз внимательно взгляните на картинку

Вы обратили внимание на то, что на этой (видимой нашему глазу) стороне автобуса нет двери. Это означает, что она должна быть на другой стороне! А если дверь находится на другой стороне, тогда автобус движется в сторону А.

Зачем решать логические загадки?

При решении логических задачек и поиске «отгадки» у человека начинают работать оба полушария мозга. Левое полушарие отвечает за логику и стремится разобраться в причинных связях. Правое несет ответственность за интуицию, учится строить целостную картину и формировать образное мышление.

У современных людей левое полушарие включается в работу не так часто — «загуглили» и отправились по делам. И, конечно, свою “логическую мышцу” можно и нужно тренировать — тут нам и пригодятся загадки на логику – они помогают держать мозг в тонусе даже в самые «ленивые» дни.

Эффект от «логических тренировок» даст о себе знать уже после первых занятий — натренированный мозг быстрее соображает, позволяя решать не только математические задачи, но и находить выход из жизненных ситуаций.

Сложные логические загадки и задачки

Что не является вопросом, но требует ответа?

Звонок в двери или по телефону.

Из половины коробки с деталями у робота Клапана получается 3 фигурки роботов.
Сколько фигурок он сможет сделать из 2 таких коробок?

12.

Когда всё видишь, то её не видишь,
А когда ничего не видишь, то её видишь.

Темнота.

Зайка очень любит шутить. Он задал маме такую загадку:
«Если бы я был тяжелее медведя, но легче божьей коровки, кто был бы самым лёгким?»

Медведь.

Что вчера было «завтра», а завтра будет «вчера»?

«Сегодня».

Профессор решил угостить друзей своим фирменным овощным салатом.
Для этого ему понадобилось: перца — 3 штуки и столько же помидоров; огурцов меньше, чем помидоров, но больше, чем редисок.
Сколько всего штук разных овощей использовал Профессор в салате?

Дед Вруниш (всегда лжёт) и дед Правдиш (говорит только правду) решили взять домой одного бездомного кота.
Правдиш: Рыжего кота брать не будем.
Вруниш: Возьмём белого.
Какого кота возьмут в дом?

Чёрного.

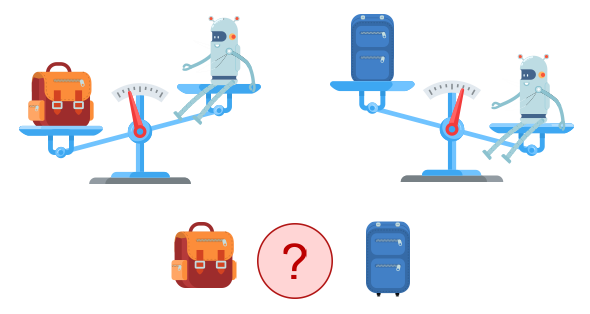
Что тяжелее: рюкзак или чемодан?

Подсказка

Сперва сравни массу Клапана с массой чемодана и рюкзака.

Источники

https://umnazia.ru/blog/all-articles/15-slozhnyh-zagadok-na-logiku
https://logiclike.com/math-logic/zagadki-na-logiku
https://logiclike.com/math-logic/zagadki-na-logiku/slozhnye
https://fishki.net/2518167-6-samyh-slozhnyh-golovolomok—pod-silu-lishy-ocheny-umnym.html
https://europaplus.ru/news/6-zadachek-kotorye-ne-mogut-reshit-vzroslye
https://4brain.ru/blog/logicheskie-zadachi/
https://Lifehacker.ru/zadachi-na-logiku/
https://Lifehacker.ru/logicheskie-zadachi/
https://thecode.media/die-hard/
https://malchishki-i-devchonki.ru/smeshnye-logicheskie-zagadki-s-otvetami-s-podvohom-i-shutochnye.html
https://multi-mama.ru/ochen-slozhnye-zagadki-s-otvetami/

Сложные загадки на логику с ответами

Каких камней не бывает в речке?

(Ответ: Сухих)

***

Загадка

Что не вместится даже в самую большую кастрюлю?

(Ответ: Крышка от нее)

***

Загадка

Что может в одно и то же время стоять и ходить, висеть и стоять, ходить и лежать?

(Ответ: Часы)

***

Загадка

Ползут 3 черепахи.1-я черепаха говорит: за мной ползут две черепахи.
2-я черепаха говорит: за мной ползёт одна черепаха и передо мной ползёт одна черепаха. А 3-я черепаха: передо мной ползут две черепахи, и за мной ползёт одна черепаха.

Как такое может быть?

(Ответ: Черепахи ползут по кругу)

***

Загадка

На ферме было 2 коня, 1 кролик, 1 щенок, 1 кошка, свинья и поросенок, корова и теленок, индюк и гусь.
Пришел Хозяин с собакой. Сколько на ферме стало ног?

(Ответ: 2)

***

Загадка

Где впервые был обнаружен картофель?

(Ответ: В земле)

***

Загадка

По чему ходят часто, а ездят редко?

(Ответ: По лестнице)

***

Загадка

Какой пробкой нельзя заткнуть ни одну бутылку?

(Ответ: Дорожной)

***

Загадка

Когда человек имеет столько глаз, сколько дней в году?

(Ответ: 2 января)

***

Загадка

Как поймать тигра в клетку?

(Ответ: Тигра в клетку не бывает, тигр в полоску)

***

Загадка

Что принадлежит вам, однако другие этим пользуются чаще, чем вы сами?

(Ответ: Ваше имя)

***

Загадка

Чем больше из нее берешь, тем больше она становится. Что это?

(Ответ: Яма)

***

Загадка

Вы сидите в самолете, впереди вас лошадь, сзади автомобиль. Где вы находитесь?

(Ответ: На карусели)

***

Загадка

Скажешь «не приходи!» — всё равно приходит. Скажешь «не уходи!» — всё равно уходит. Что это такое?

(Ответ: Время)

***

Загадка

Странный дождь порой идет: сотней струй он кверху бьет.

(Ответ: Фонтан)

***

Порядок выполнения математических операций

При решении математических задач необходимо соблюдать определенный порядок выполнения операций. Это позволяет получить правильный ответ и избежать ошибок.

Существует следующий порядок выполнения математических операций:

Выполнение операций в скобках.
Выполнение операций с унарными знаками (плюс, минус).
Выполнение операций умножения и деления.
Выполнение операций сложения и вычитания.

Данный порядок можно запомнить с помощью аббревиатуры СУМД.

Применяя данный порядок, можно решить пример 6:2(1+2) следующим образом:

Таким образом, ответ на данный пример равен 9.

Важно отметить, что некоторые задачи могут иметь несколько возможных вариантов решения в зависимости от порядка выполнения операций. Например, в примере 2+3*4 можно сначала выполнить умножение, а затем сложение, получив ответ 14, или наоборот, получив ответ 20

Однако, существуют задачи, в которых порядок выполнения операций не имеет значения. Например, в примере 2*3+4*5 можно сначала выполнить умножение, а затем сложение, или наоборот, получив в обоих случаях ответ 22.

Соблюдение порядка выполнения математических операций является важным условием получения правильного ответа на задачу.

Загадки для взрослых — с подвохом: лучшая подборка

Загадки с подвохом прекрасный способ повеселиться. Правда помните, что подобный тип загадок для взрослых часто имеет слегка пошлый уклон, а потому выбирать их для развлечения нужно только в том случае, если планируется встреча близких друзей.

Загадки для взрослых — с подвохом:

Самый известный полупроводник. (Ответ — Сусанин.)
Что нужно сделать, если вы сели в машину, а ноги до педалей не достают? (Ответ — можно попробовать пересесть на водительское место.)
А что нужно сделать, если вы сели на водительское кресло, а ноги до педалей по-прежнему не достают? (Ответ — надо для начала повернуться лицом к рулю.)
Что нужно делать, когда увидишь зеленого человечка? (Ответ — быстро переходить улицу, пока горит зеленый цвет светофора.)
Может ли страус назвать себя птицей? (Ответ — мог бы, если бы умел разговаривать.)
Вы сидите в самолете, перед вами находится лошадь, сзади автомобиль. Где вы находитесь? (Ответ — в парке отдыха, на каруселях.)
В каком случае шесть детей, две собаки, четверо взрослых, забравшись под один зонтик, не намокнут? (Ответ — все очень просто, если на улице не будет дождика.
Имя первой женщины в мире, идеально освоившей летательный аппарат. (Ответ — Баба Яга.)
Эти три телезвезды хорошо известны каждому из нас. Блондина зовут Степан, шатена зовут Филипп. А как зовут лысого? (Ответ — всем известный Хрюша.)
В корзине имеется 5 грибов. Как разделить грибы между пятью грибниками, чтобы каждому досталось поровну, и один гриб остался бы в корзине? (Ответ — 4 грибника получат по одному грибу, а пятый получит корзину с одним грибом.)
Два мальчика играли в шашки. Каждый из них сыграл пять партий, и каждый выиграл такое же количество игр. Как такое могло произойти? (Ответ — просто они играли с разными противниками.)

Мальчик заплатил за бутылку с пробкой 11 рублей. Бутылка стоит на 10 рублей больше, чем пробка. Сколько стоит пробка?

(Ответ: 50 копеек)

***

Загадка

По чему ходят часто, а ездят редко?

(Ответ: По лестнице)

***

Загадка

Идет то в гору, то с горы, но остается на месте.

(Ответ: Дорога)

***

Загадка

Летели галки, сели на палки. Сядут по одной — галка лишняя, сядут по две — палка лишняя. Сколько было палок и сколько было галок?

(Ответ: 3 палки, 4 галки)

***

Загадка

Где встречается такое, что конь через коня перепрыгивает?

(Ответ: В шахматах)

***

Загадка

Два пятиклассника Петя и Алёнка идут со школы и разговаривают.
— Когда послезавтра станет вчера, — сказал один из них, — то сегодня будет так же далеко от воскресенья, как и тот день, который был сегодня, когда позавчера было завтра. В какой день недели они разговаривали?

(Ответ: Воскресенье)

***

Загадка

Какой пробкой нельзя заткнуть ни одну бутылку?

(Ответ: Дорожной)

***

Загадка

Они бывают металлические и жидкие. О чем речь?

(Ответ: Гвозди)

***

Загадка

У кого за носом пятка?

(Ответ: Обувь)

***

Загадка

В автобусе ехали 20 человек. На первой остановке вышли 2 и вошли 3 человека, на следующей — 1 вышел и 4 вошли, на следующей — 5 вышли и 2 вошли, на следующей — 2 вышли и 1 вошел, на следующей — 9 вышли и никто не вошёл, на следующей — ещё 2 вышли. Вопрос: сколько было остановок?

(Ответ: 6)

***

Загадка

На столе лежит 100 листов бумаги.
За каждые 10 секунд можно посчитать 10 листов.
Сколько секунд понадобится, чтобы посчитать 80 листов?

(Ответ: 20)

***

Загадка

Марина мечтала о шоколадке, но ей на покупку не хватало 10 рублей. Вася тоже мечтал о шоколадке, но ему не доставало всего 1 рубля. Дети решили купить хотя бы одну шоколадку на двоих, но им все равно не хватило 1 рубля. Какова стоимость шоколадки?

(Ответ: Стоимость — 10 рублей. У Марины нет денег вообще.)

***

Загадка

Что можно взять в левую руку, но нельзя в правую?

(Ответ: Локоть правой руки)

***

Загадка

За столом сидят ковбой, джентльмен и йог. Сколько ног стоит на полу?

(Ответ: 1 нога (ковбой кладет ноги на стол, джентльмен кладет ногу на ногу,а йог медитирует)

***

Загадка

С какой птицы нужно ощипать перья, чтобы получились сразу утро, день, вечер и ночь?

(Ответ: С утки (сутки)

***

Ответ

Монти Холл и три шкатулки

Если пустую шкатулку открыли случайно

Пустую шкатулку выбрали специально

Как решается пример

Бабушка и помидоры

Комментарии

Странный разговор двух программистов

Задача №5

Какие есть варианты решения

Почему знак умножения опускается

Как решается пример

Почему пример 36:3(8-6)/6 некорректен

Решение примера

Программисты и странное знакомство

Задача для детей 7 лет

Зачем решать логические загадки?

Сложные логические загадки и задачки

Сложные загадки на логику с ответами

Порядок выполнения математических операций

Загадки для взрослых — с подвохом: лучшая подборка

Похожие записи:

Похожие записи: